Measuring Thinking Efficiency in Reasoning Models: The Missing Benchmark

Large Reasoning Models (LRMs) employ a novel paradigm known as test-time scaling, leveraging reinforcement learning to teach the models to generate extended chains of thought (CoT) during reasoning tasks. This enhances their problem-solving capabilities beyond what their base models could achieve independently.
While cost and efficiency trade-off curves ("the Pareto frontier") typically focus on model intelligence versus cost per million completion tokens, token efficiency — the number of tokens used for reasoning relative to the solution — is a critical factor that is recently receiving more attention.
Anecdotal evidence suggests open weight models produce significantly more tokens for similar tasks than closed weight models.
This report systematically investigates these observations. We confirm this trend to be generally true, but observe significant differences depending on problem domain.
TL;DR:
Closed models (OpenAI, Grok-4) optimize for fewer tokens to cut costs, while open models (DeepSeek, Qwen) use more tokens, possibly for better reasoning. Open weight models use 1.5–4× more tokens than closed ones (up to 10× for simple knowledge questions), making them sometimes more expensive per query despite lower per‑token costs. OpenAI leads in token efficiency for math. Among open models,
llama-3.3-nemotron-super-49b-v1
is most efficient, while Magistral models are outliers with exceptionally high token usage. The release of OpenAI's
gpt-oss
open weight models with extremely short CoT can serve as a reference to optimize token usage in other open weight models.
Why is it of interest to measure token efficiency?
Token efficiency is a critical metric for several practical reasons:
First, while hosting open weight models may be cheaper, this cost advantage could be easily offset if they require more tokens to reason about a given problem. Second, an increased number of tokens will lead to longer generation times and increased latency. Finally, inefficient token usage may exhaust the available context window, limiting the model's ability to process complex queries effectively.
We address three questions:
- Do open weight models systematically require more tokens than closed weight models for comparable tasks?
- What are the cost implications when token efficiency is factored into total inference expenses?
- Are there specific task categories where this efficiency gap is more pronounced?
How can we measure token efficiency?
Measuring the length of the thinking process, the Chain-of-Thought, presents some issues because most recent closed source models will not share their raw reasoning traces. The rationale behind this is to prevent competitors from fine-tuning on their reasoning traces. Instead, they use smaller language models to transcribe the chain of thought into summaries or compressed representations. This means the original reasoning process remains hidden, with only the final answer and a transcribed version of the CoT available for analysis.
However, since models are usually billed by the number of output tokens for the full prompt completion (thinking and final answer output), we can use the number of completion tokens as a proxy for the total effort required to generate an answer.
To investigate which models transcribe the CoT and which make them directly available, we analyzed the relationship between total characters for completion (the sum of thinking trace and final output) versus the number of tokens billed for completion across all prompts in this study.
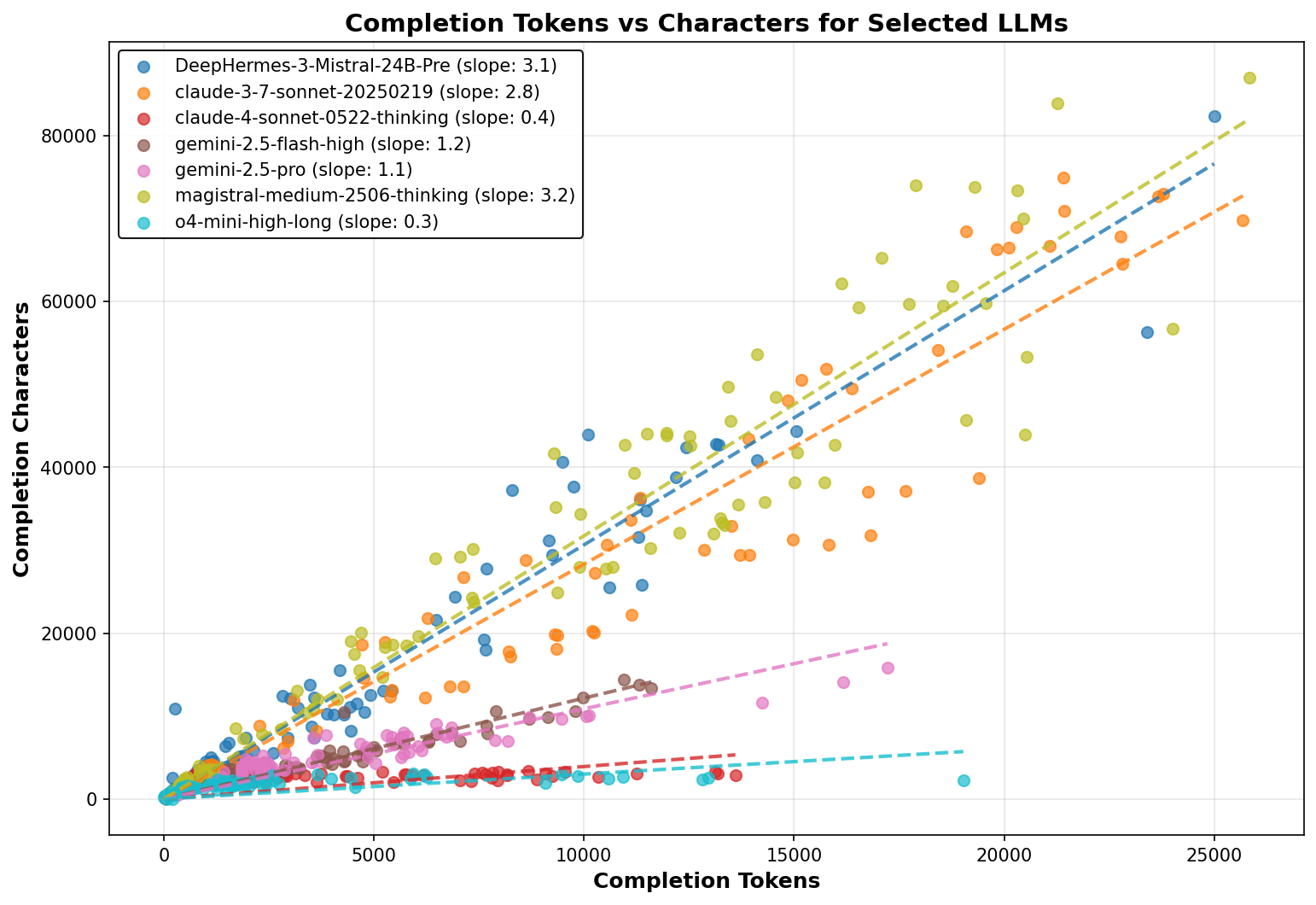
Figure 1 illustrates the relationship between total characters for completion (combining thinking trace and final output) versus the number of tokens billed for completion across all prompts in this study. Each model shows a linear relationship, but with different slopes depending on the specific model implementation.
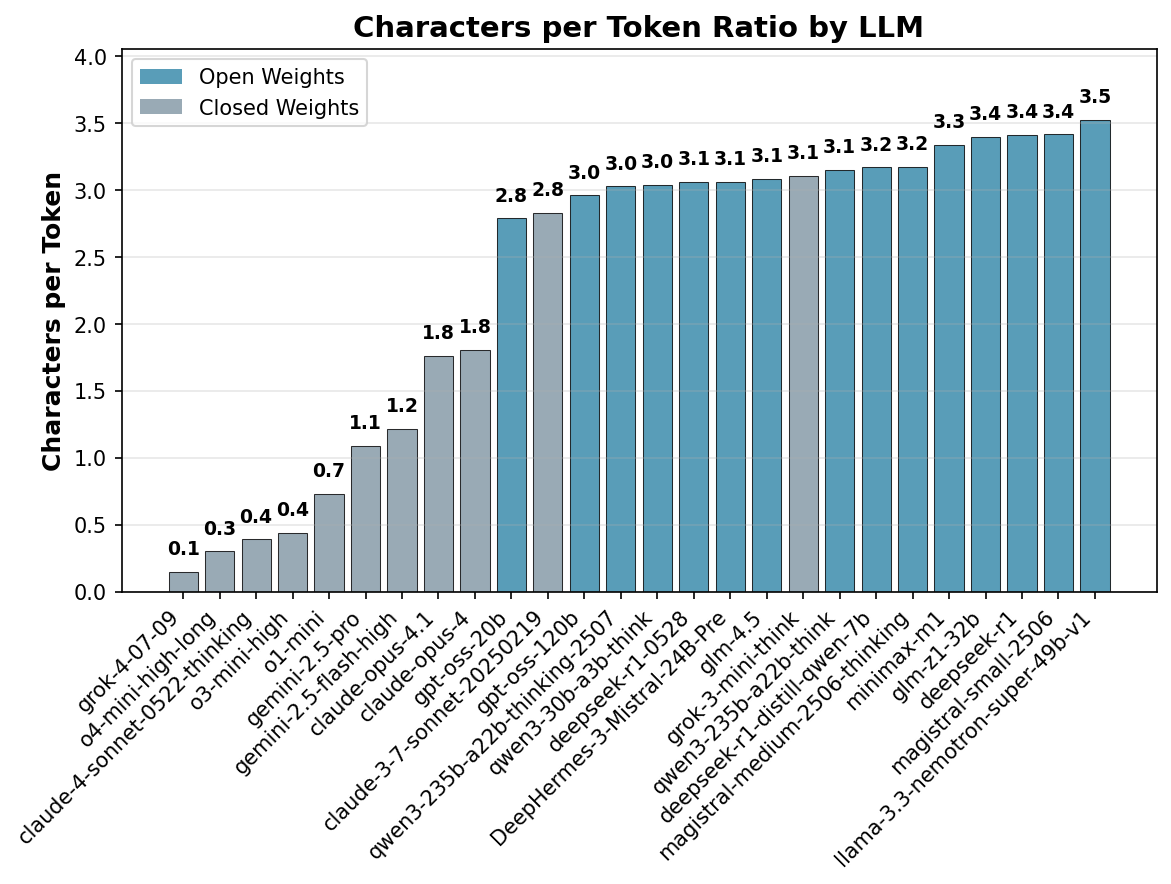
Figure 2 presents the extracted slopes for each model, revealing interesting patterns.
- Open weight models show a consistent character-to-token ratio of approximately 3-3.4, which is typical for tokenizers. This suggests that no transcription took place for these models.
- Claude 3.7 Sonnet exhibits a ratio of 2.8, suggesting that the CoT is mostly intact, but the lower ratio may indicate that some filtering took place, possibly through simple word filtering or substitution.
- Gemini models show a slope of ~1, which suggests a text densification ratio of 3:1. While the original CoT is not available, the output remains proportional to chain of thought length and should reflect the reasoning process.
- OpenAI and Claude models show a ratio of 0.3, with closer examination of the scatter plot revealing that character count doesn't increase with CoT length, suggesting only a summary of the entire CoT is provided rather than transcription. This behavior seems to be specific to chat completions, as continuous updates are seen in streaming mode.
Some models also provide information about reasoning tokens as part of the API response. However, we found this number to be unreliable in many cases as some models (Claude) would only return the number of tokens of the transcribed CoT, while others would provide token counts that exceeded the total completion length. We introduced consistency checks to decide how to extract the reasoning token count, as described in the appendix.
Based on these findings, we use completion tokens to assess overall effort, supplemented by reasoning tokens from APIs where available.
Dataset
To systematically evaluate token efficiency across different reasoning domains, we curated a dataset consisting of three categories:
- Knowledge questions: Can be answered in one sentence from the model's pre-training corpus.
- Math problems: Math problems should exhibit the most optimized behavior of reasoning models.
- Logic puzzles: Logic puzzles require both semantic understanding and logical reasoning.
The questions were chosen to be solvable within the 30,000 token limit to avoid truncated responses.
Findings
Knowledge questions
This part of the evaluation consists of 5 trivial knowledge questions that can be answered in one word and that do not require reasoning at all. E.g.
- What is the capital of Australia?
- How many days are there in February during a leap year?
All models were able to respond to these prompts correctly. The purpose of these questions is to probe for superfluous reasoning. Efficient models should be able to determine that no reasoning is required.
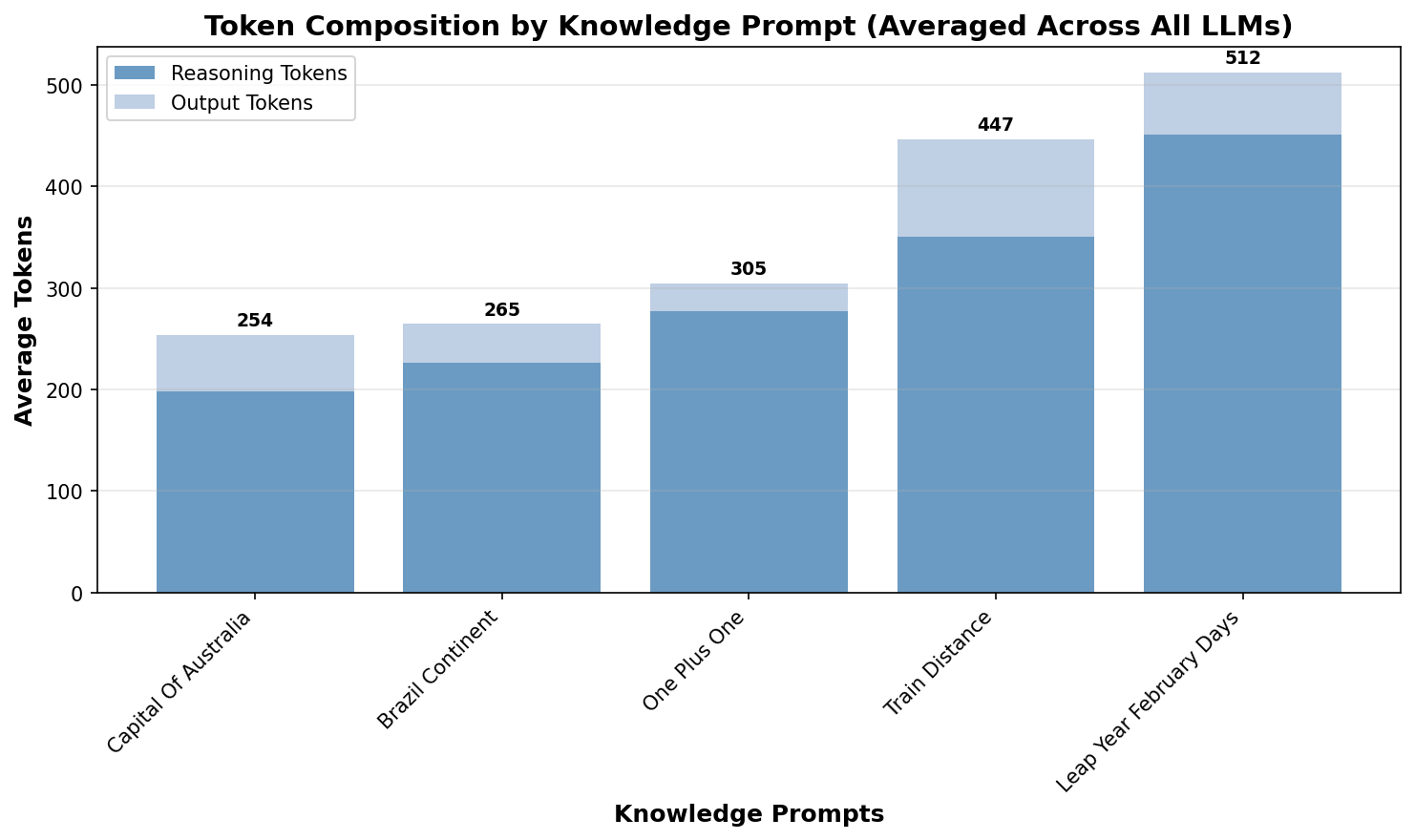
Figure 3 shows the average number of reasoning and output tokens for each prompt. We can see that, on average, reasoning models spend hundreds of tokens pondering simple knowledge questions.
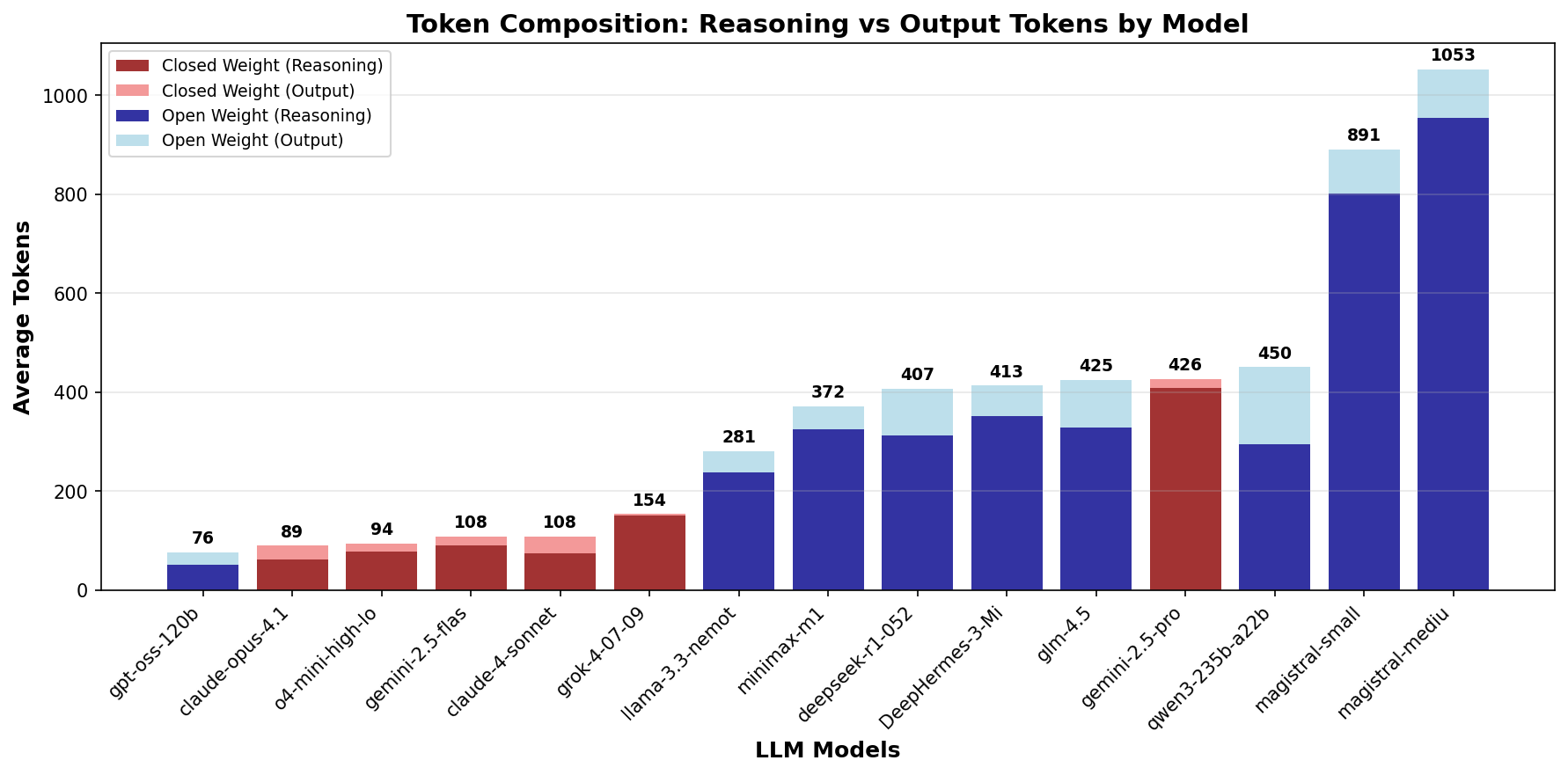
Resolving this per model reveals stark differences. Figure 4 shows that closed-weight frontier lab models are far more token efficient than open weight models.
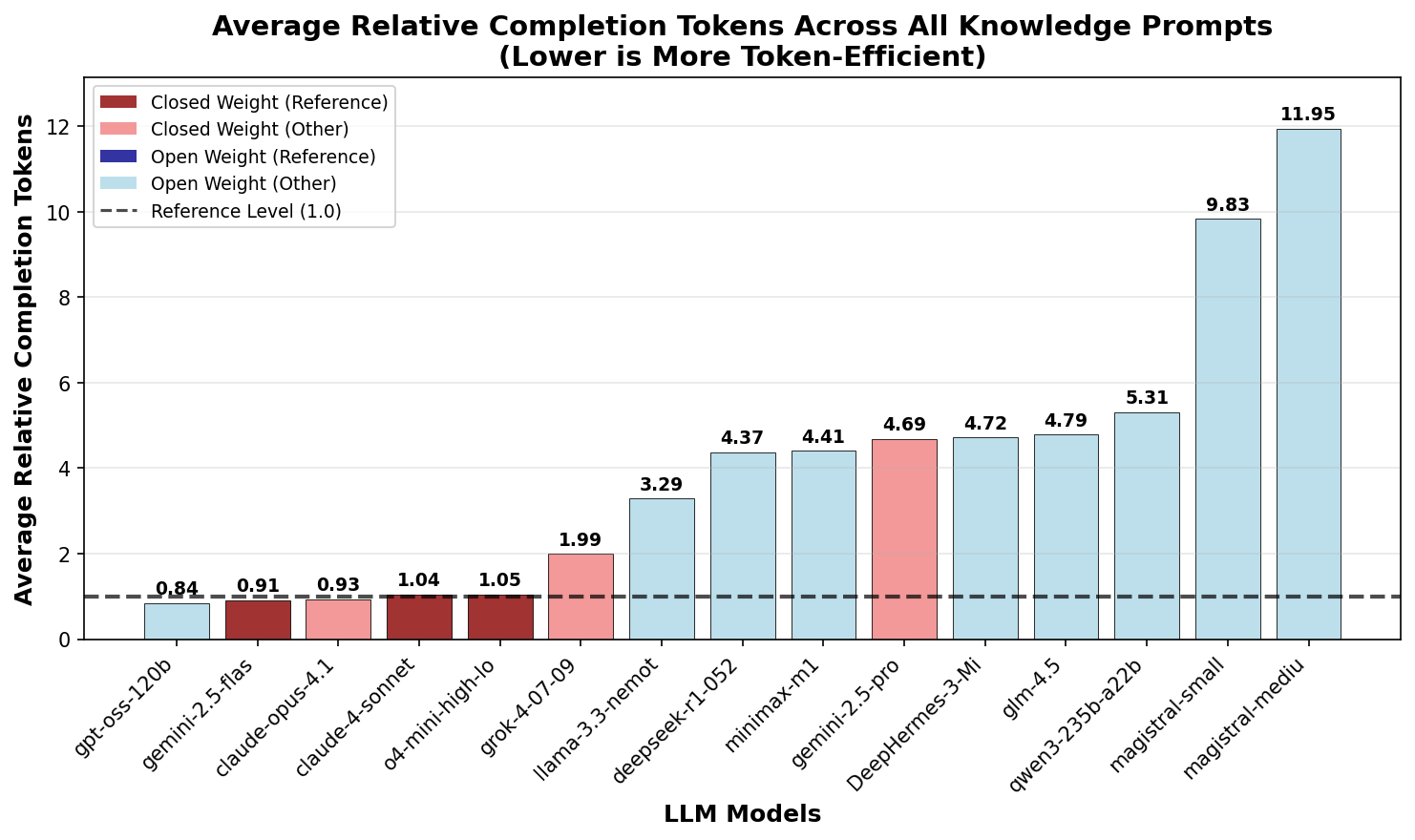
To better quantify the excess token ratio, we normalized the token count for each prompt relative to the most optimized closed weight models (reference). This approach considers the excess token ratio for all prompts equally, which contrasts with averaging across all completion lengths, which would be dominated by long completions.
Figure 5 shows the mean excess token
ratio for different LLMs. The recently released Magistral
models are an extreme outlier with up to 10x excess tokens.
We also see that most other open weight models show an
excess token ratio of around 4, meaning that they use four
times as many tokens as the most optimized closed weight
models. The recently released
gpt-oss-120b by OpenAI leads all
other models in token efficiency.
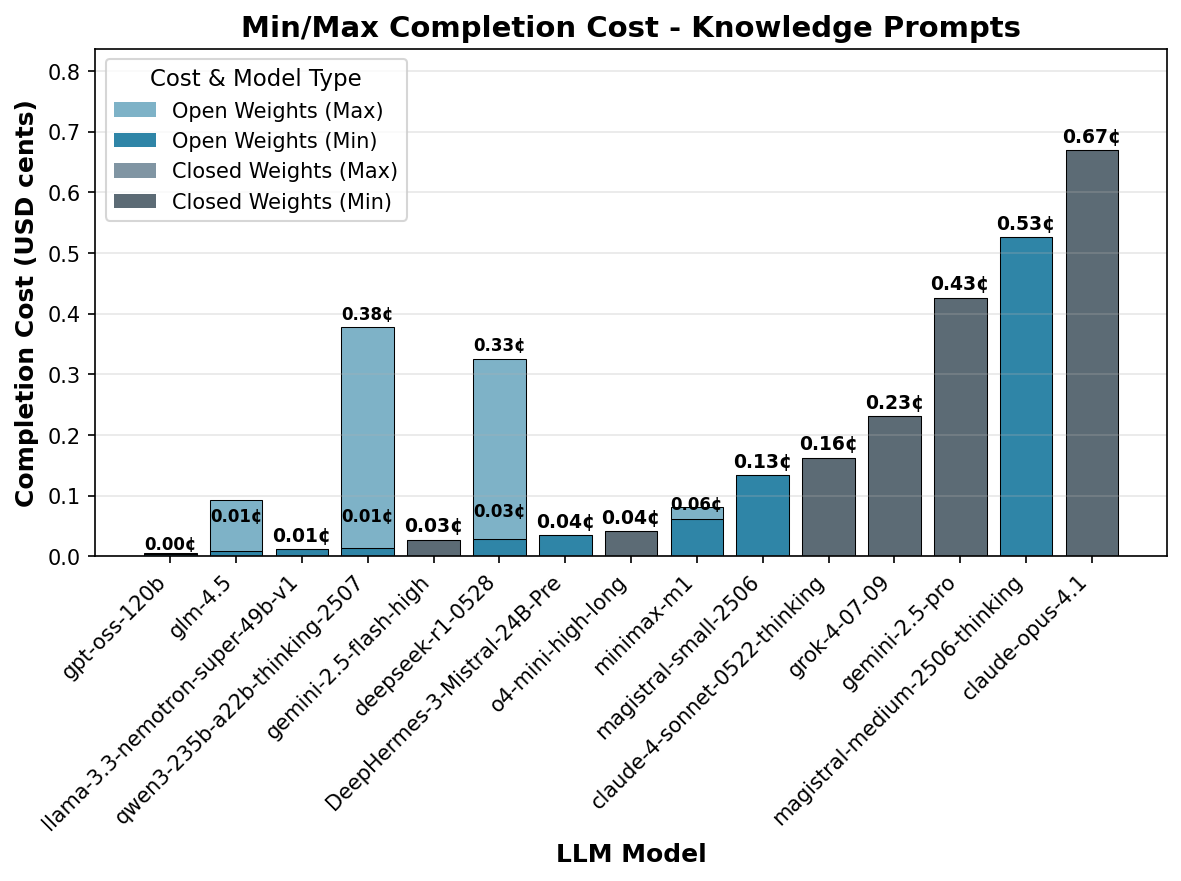
How does this affect inference costs? Figure 6 shows the mean cost per model for knowledge questions, based on minimum and maximum completion pricing on the OpenRouter API in July 2025. The better token efficiency of closed weight models often compensates for the higher API pricing of those models.
Math problems
Most reasoning models are specifically trained to solve mathematical problems. One reason for this is that math problems are usually easily verifiable, which is a key advantage for reinforcement learning. Furthermore, math problems are also an easy benchmark target for reasoning models as there are many widely available problem sets.
For this study, we selected a set of six problems to test token efficiency in the math domain. Three problems were sourced from AIME 2025, and one problem was taken from AIME 2023. Easier problems were chosen to prevent models from exceeding the 30,000 token limit. To further investigate the role of memorization in problem-solving, we created two modified problems by changing the variables in one AIME 2025 problem and the AIME 2023 problem. The rationale behind this approach is that unknown problems may require a longer chain of thought, as the model cannot rely on memorized solutions. The AIME 2025 problems are too new to be in the pre-training data of any model, while some may have seen the AIME 2023 problems during pre-training.
Example
AIME2025I Problem 2 (Original)
Find the sum of all positive integers $n$ such that $n+2$ divides the product $3(n+3)(n^2+9).$
AIME2025I Problem 2 (Modified)
Find the sum of all positive integers $n$ such that $n+2$ divides the product $3(n+3)(n^2+7).$
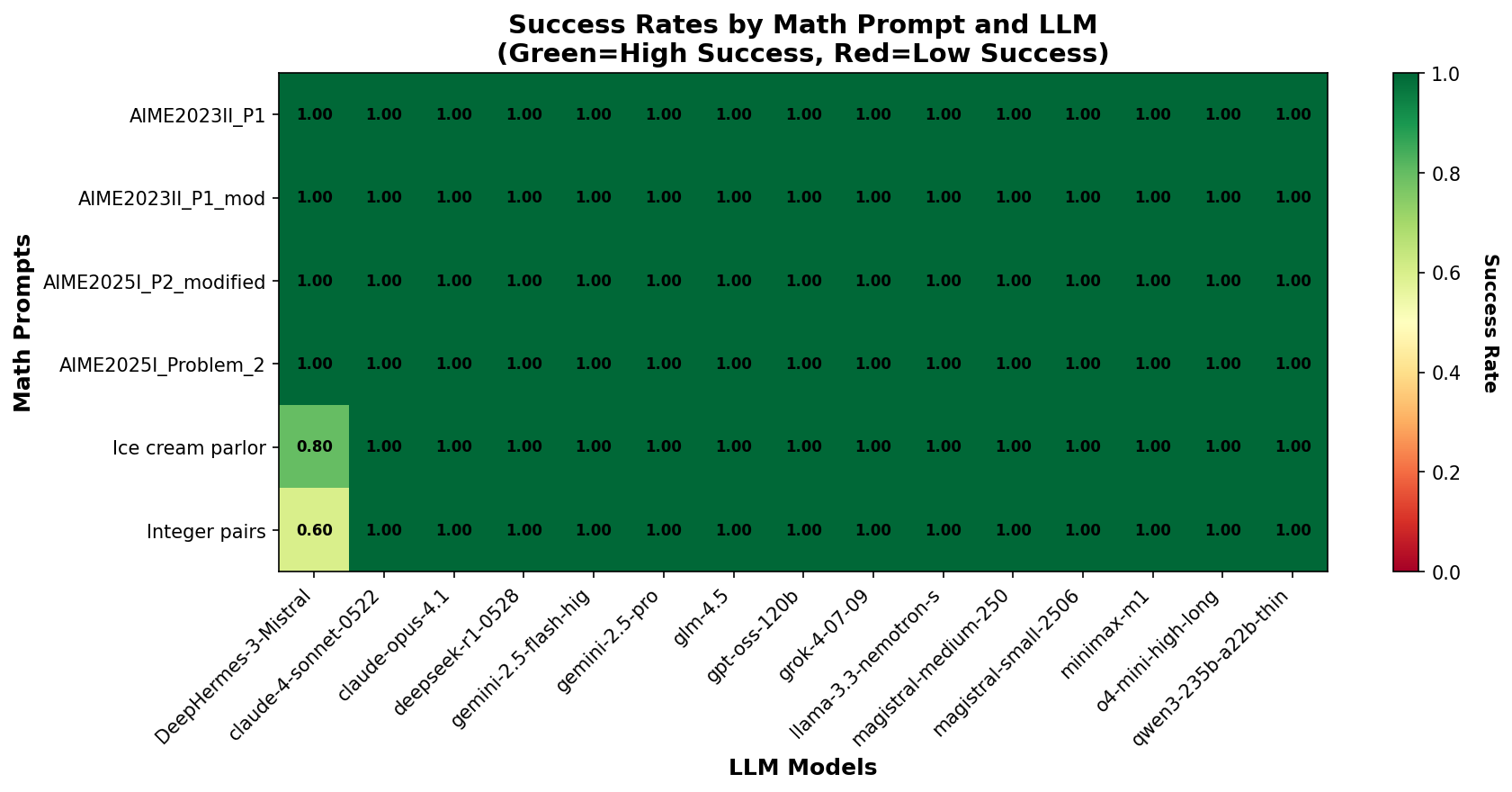
With a few exceptions, all models were able to solve the math problems correctly Figure 7.
We can see that, on average, fewer than 10,000 tokens are required to solve the selected problems (Figure 8). The more complex problems from the AIME2025 set would easily require more than 30,000 tokens in some models and were therefore not used for this evaluation to avoid skewing the distribution due to truncation.
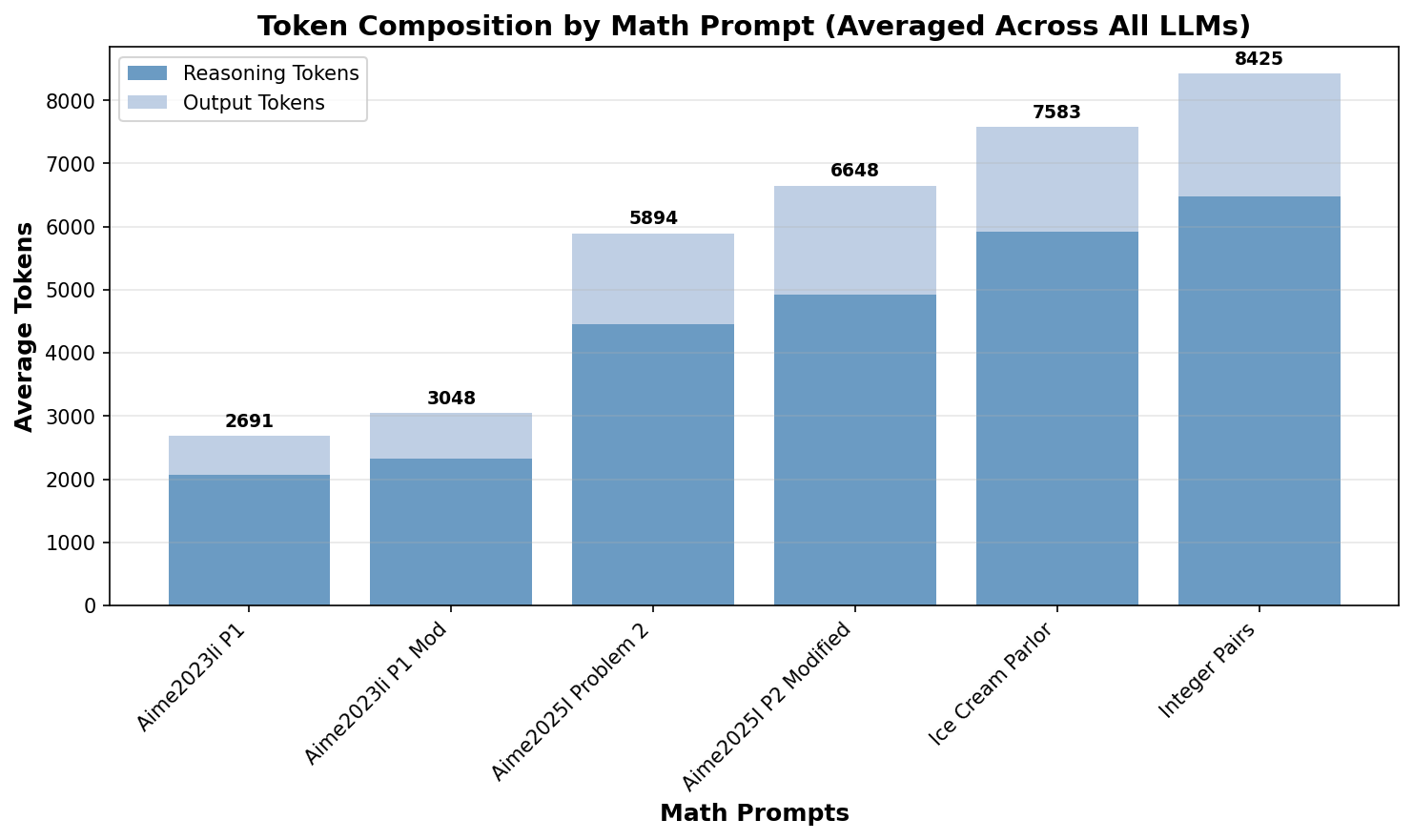
Remarkably, the number of tokens required to solve the pairs of original and modified problems is almost identical. This could suggest two trends across all LLMs:
- These math problems are not solved based on memorization, but algorithmically.
- The number of tokens is identical for similar problems.
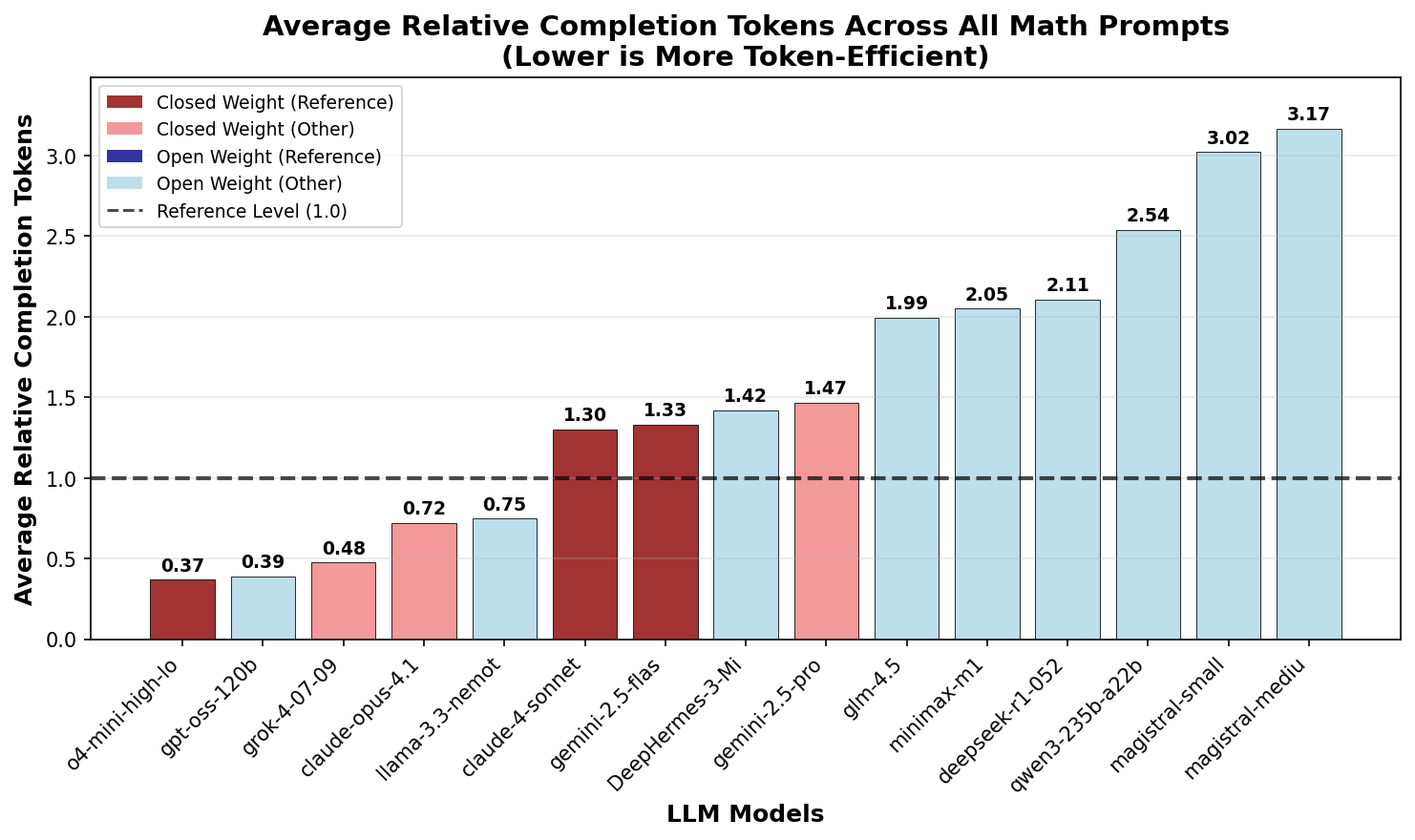
Figure 9 shows the relative excess
token ratio compared to the reference. In contrast to the
trends observed for knowledge questions, the relative ratio
between models is much lower.
o4-mini-high-long is a notable
outlier with a surprisingly low token count — 3x fewer
tokens than other commercial models. This suggests that
o4-mini has been specifically optimized for token efficiency
in mathematical problems. The same optimizations seem to be
shared by the OpenAI open weight model
gpt-oss-120b. The recently
released grok-4 also seems to
have been optimized for token efficiency in math problems.
The most efficient open weight model is
llama-3.3-nemotron-super-49b-v1,
which uses fewer tokens than most closed weight models.
magistral-small and
magistral-medium remain the
highest token count models, but show only 3x the ratio of
the reference models.
Generally, there is a very clear trend toward higher reasoning token usage for open weight models in math problems, compared to closed weight models. This may suggest an optimization toward benchmarking performance rather than production efficiency.
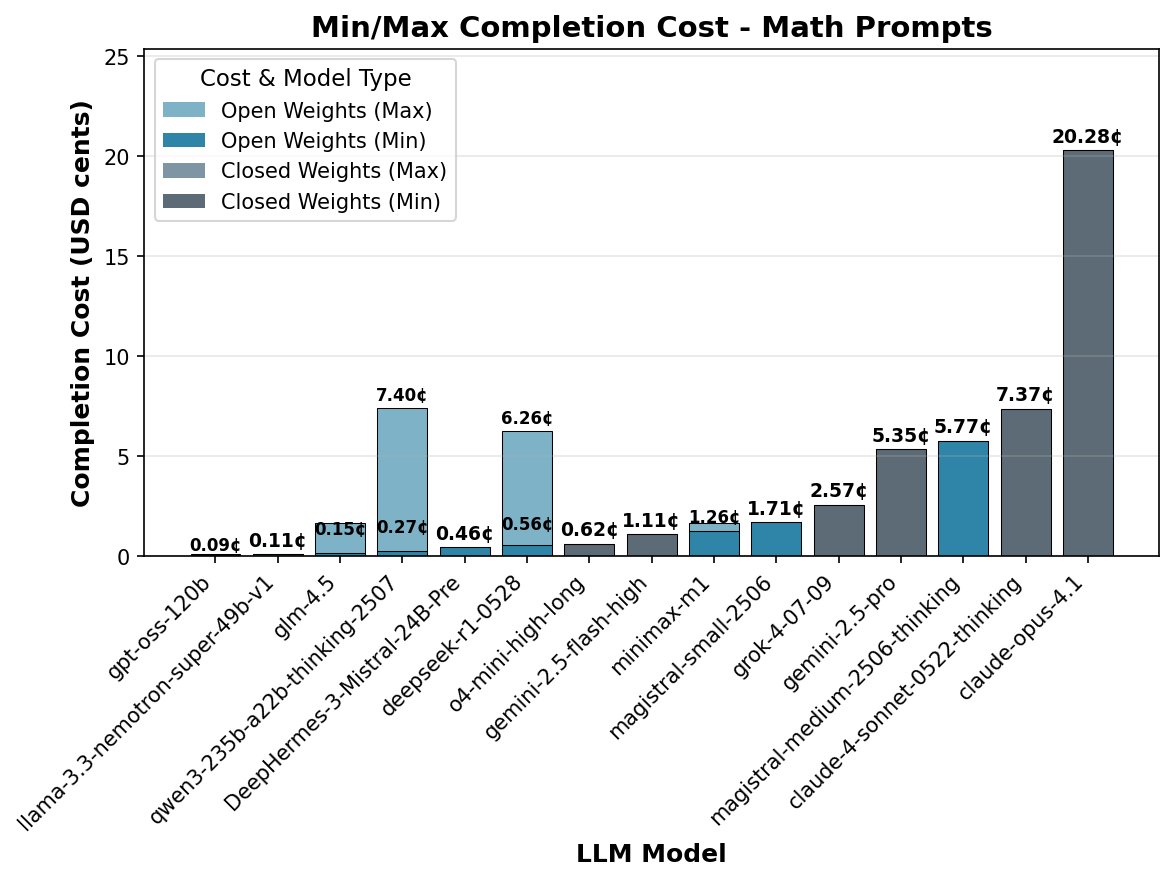
Examining completion costs reveals that since token
consumption is relatively similar across most models for
math problems, those with higher per-token pricing naturally
incur the highest completion costs. However, the exceptional
token efficiency of
o4-mini-high-long and
gpt-oss-120b enables them to
achieve very competitive total completion costs despite
potentially higher per-token costs, demonstrating how
optimization can offset pricing disadvantages.
Logic puzzles
Logic puzzles are a curious domain for reasoning models. They require a combination of semantic understanding and logical reasoning, making them an interesting test case for evaluating reasoning capabilities.
However, many well-known logic puzzles are commonly found in pre-training data, which causes models to be over-fitted on specific solutions. Non-reasoning models will often have difficulty recognizing small changes to logic problems and tend to answer them based on memorization of the original problem. The Misguided Attention evaluation showcases this issue. Reasoning models can often overcome the bias of their pre-training data in the CoT and solve modified problems correctly.
To explore the effect of memorization, variants of two well-known logic puzzles were selected in addition to a generic logic puzzle (roses problem).
Bridge and torch problem
The bridge and torch problem requires finding the minimum time for four people with a torch to cross a bridge at night. The original problem and three variants were included:
| Problem Variant | Description |
|---|---|
| bridge_torch_default | The unmodified problem in its most well-known version with a 17-minute solution |
| bridge_torch_easy | Ambiguous version where two solutions exist: 10 and 17 minutes |
| bridge_torch_easy_10m | Simplified version with a 10-minute solution |
| bridge_torch_impossible | Constraints that make the problem impossible to solve |
Generally, we found that even more recent reasoning models struggle with logic problems that have ambiguous or impossible solutions.
Monty Hall problem
The Monty Hall problem is a very well-known and famously unintuitive probability puzzle. All base models used for reasoning models are severely over-fitted on this problem and are biased toward solutions of the Monty Hall problem even for remotely similar scenarios.
The original problem and two variants were included:
| Problem Variant | Description |
|---|---|
| monty_hall_default | The unmodified Monty Hall problem |
| monty_hall_inverse | A modified version of the Monty Hall problem with the opposite solution |
| monty_appliance_simple | An ambiguous problem that can be easily answered by humans, but is usually answered in the context of the Monty Hall problem by reasoning models |
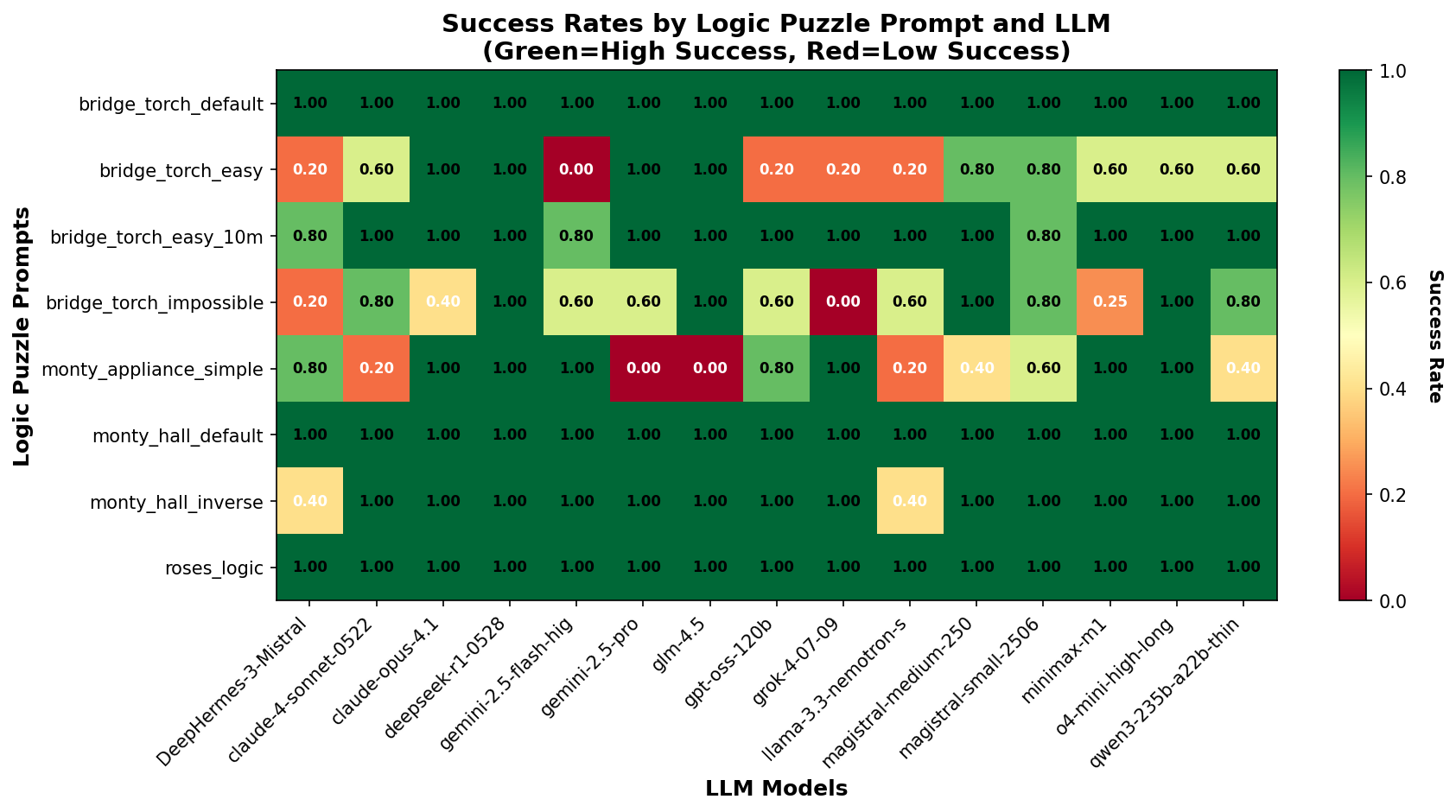
Figure 10 shows the success rates across different logic puzzle problems. Unlike the math problems, success rates vary significantly across both models and problem types. Only the default problems were solved by all models, while many models struggle with modified problems, indicating strong influence of pre-existing bias in the model.
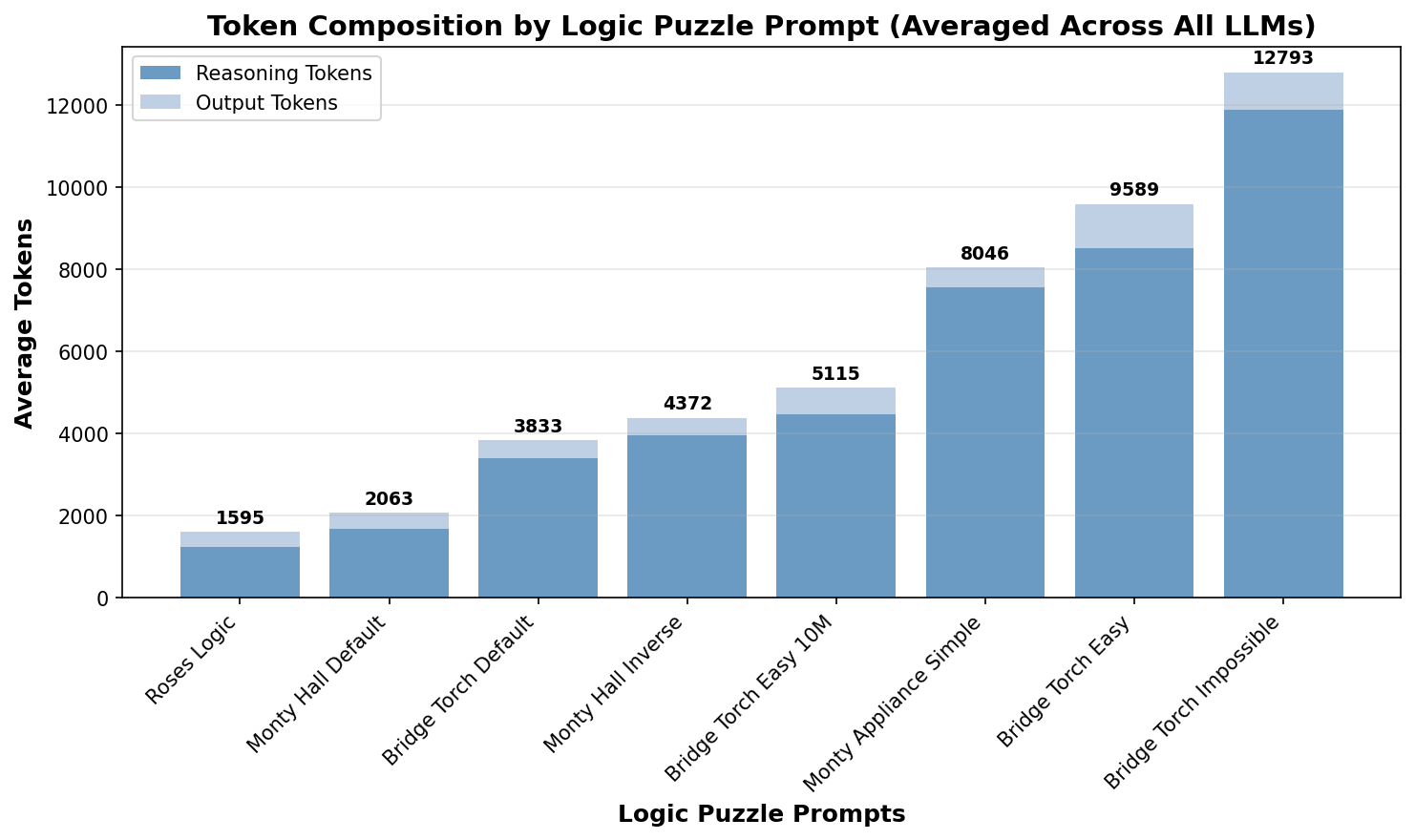
Figure 11 shows the average token consumption for all prompts. Remarkably, the number of reasoning tokens is the lowest for the default problems, while it significantly increases for modified problems. This is unlike the observation for math problems and suggests that pre-existing bias allows solving the problems with a shorter CoT for the default problems. The impossible problem generates the longest CoT as the models tend to try many solutions before giving up.
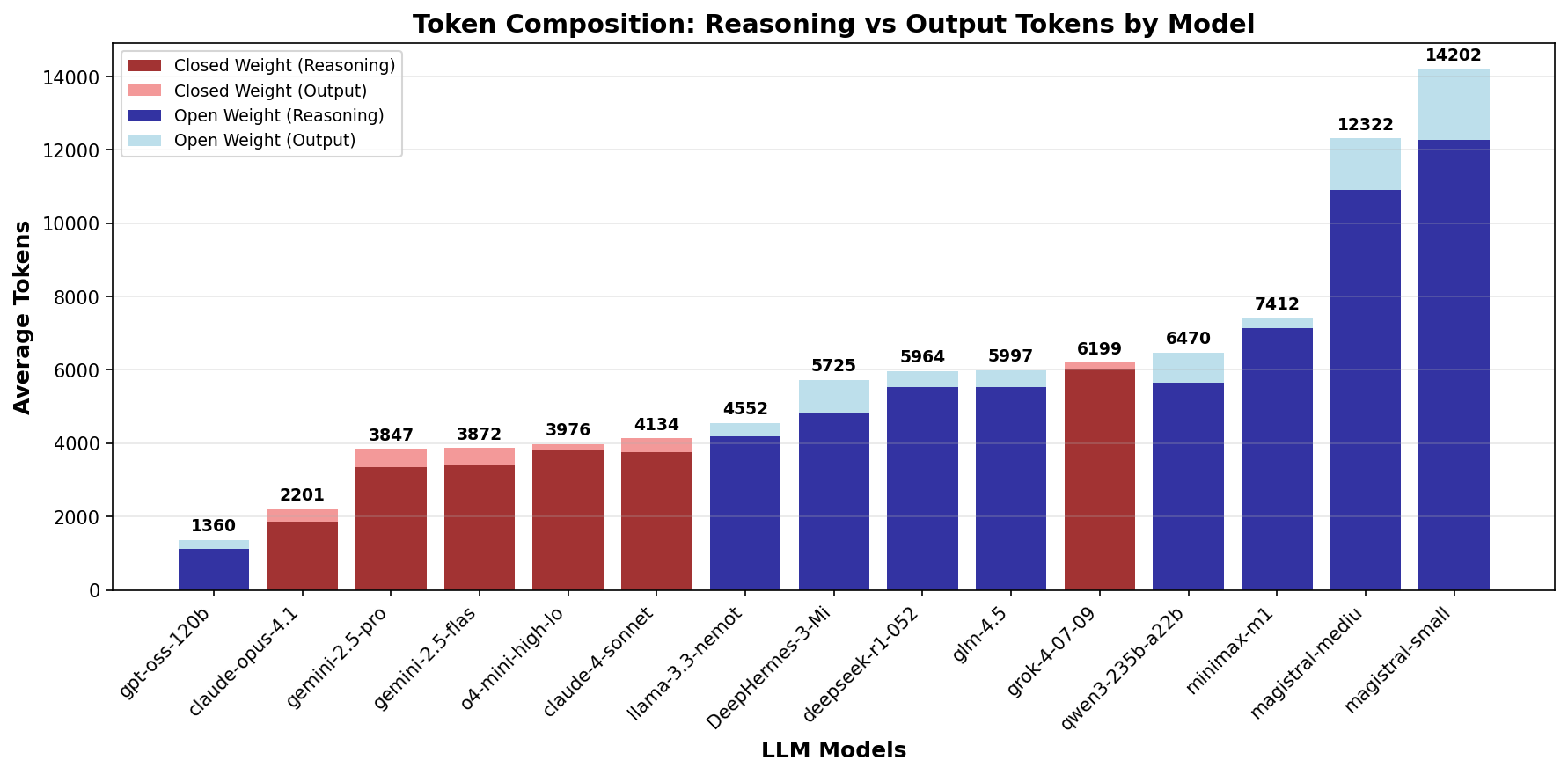
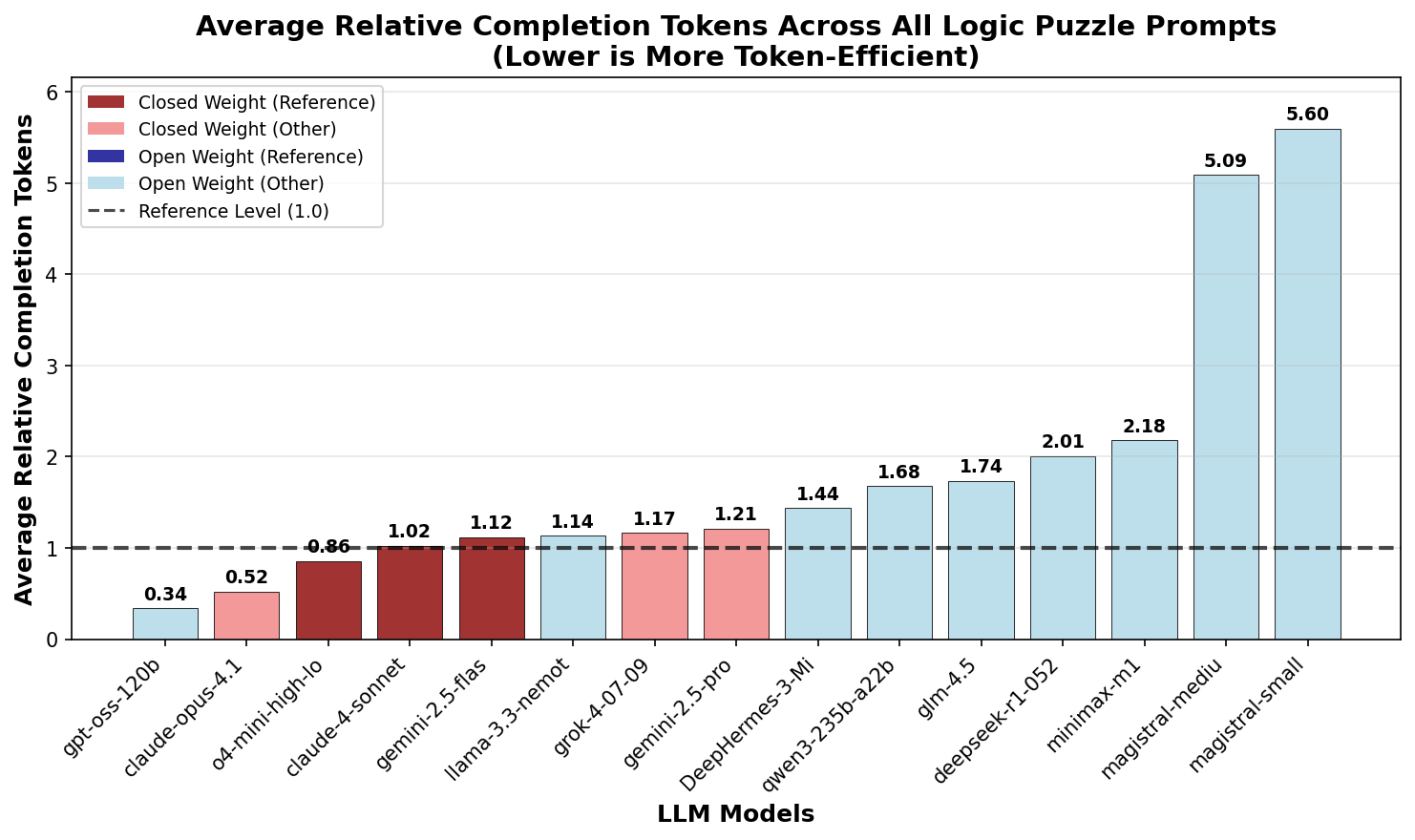
Similar to the patterns observed in other categories,
Figure 12 shows that open-weight
models use more tokens than closed-weight models for logic
puzzles. However, the gap is far less pronounced than for
math and knowledge questions.
magistral-small and
magistral-medium still present an
exception for high token usage.
claude-opus-4 uses the fewest
reasoning tokens, a trend generally observed across problem
domains. The extreme token optimization that was observed
for o4-mini-high cannot be seen
for logic puzzles.
Similar to the math domain, Nvidia's model
llama-3.3-nemotron-super-49b-v1
stands out as the most token efficient open weight model
before the release of
gpt-oss-120b.
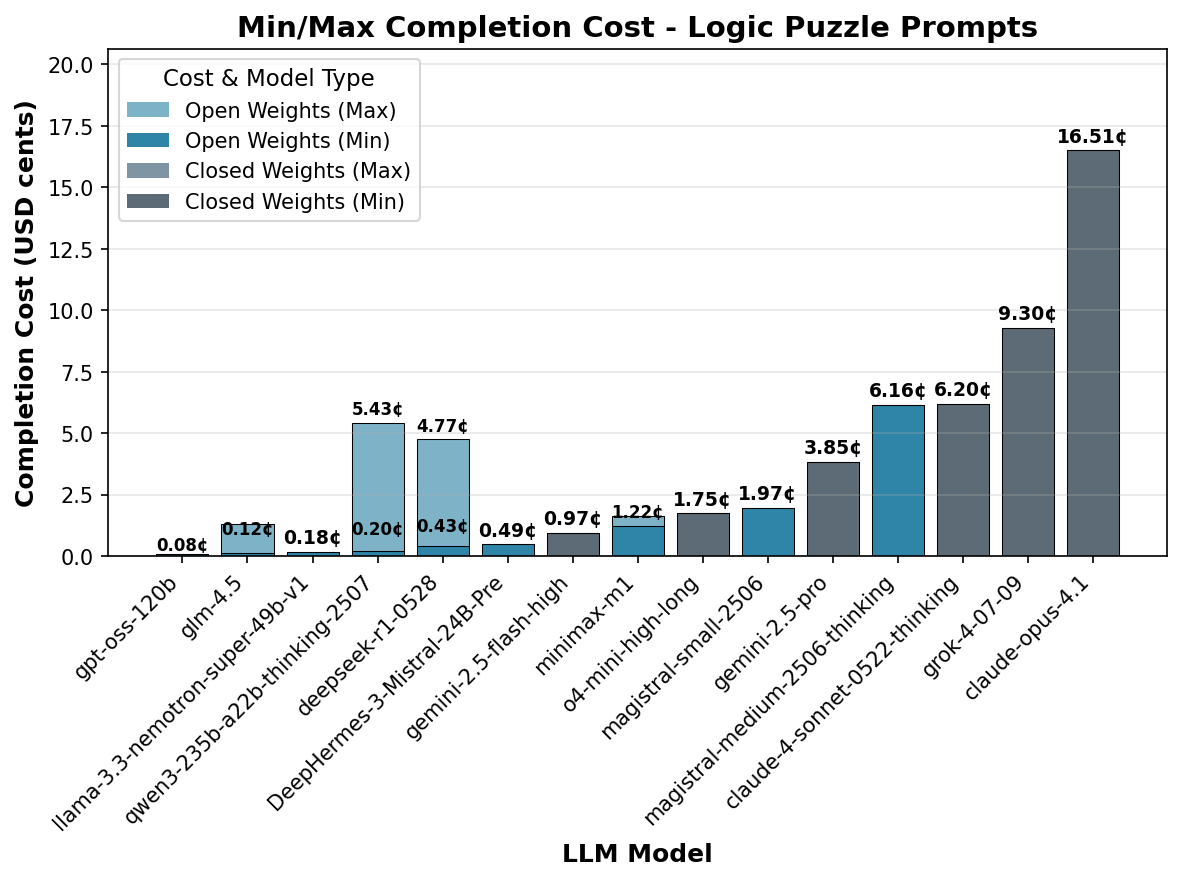
The cost analysis for the logic puzzle prompts reveals few surprises; since the variation in tokens is modest for logic prompts, the completion cost mostly scales with token pricing.
Chain of Thought Optimization
Since the chain of thought of
gpt-oss-120b is freely
accessible, it allows us to inspect some of the length
optimizations that are likely also part of the other OpenAI
models. Below, we compare the CoT of
gpt-oss-120b with the CoT of
Deepseek-R1-0528 for selected
knowledge, math and logic prompts.
Knowledge
Question
PROMPT
Which continent is Brazil located on?
RESPONSE DeepSeek R1-0528
Okay, the user is asking which continent Brazil is located on. This seems like a straightforward geography question. Hmm, I recall that Brazil is the largest country in South America. Let me double-check that fact to be sure. Yes, definitely South America. The user just wants a simple answer without any extra details, so I'll keep it concise. No need to mention neighboring countries or other continents. I wonder if they're asking for a school assignment or just casual curiosity. Either way, the answer is clear. Should I add that it's in the southern hemisphere? No, the question only asks for the continent. Best to stick to what was asked. "South America" it is. Short and accurate.
RESPONSE gpt-oss-120b
The user asks: "Which continent is Brazil located on?" Answer: South America.
We can see that
gpt-oss-120b omits a lot of
superfluous reasoning and directly provides the answer.
Math
Question (AIME2023II P1)
PROMPT
The numbers of apples growing on each of six apple trees form an arithmetic sequence where the greatest number of apples growing on any of the six trees is double the least number of apples growing on any of the six trees. The total number of apples growing on all six trees is $990.$ Find the greatest number of apples growing on any of the six trees.
RESPONSE DeepSeek R1-0528 (middle part omitted for brevity)
The problem states that the apples on six trees form an arithmetic sequence, with the greatest number being double the least number. The total apples are 990, and I need to find the greatest number of apples. An arithmetic sequence has each term after the first obtained by adding a constant difference. So, if I denote the first term (the least number) as \( a \), and the common difference as \( d \), then the sequence is \( a, a+d, a+2d, a+3d, a+4d, a+5d \). Since it's six trees, the terms are \( a, a+d, a+2d, a+3d, a+4d, a+5d \). The greatest number is \( a + 5d \), and it's given that this is double the least number, which is \( a \). So, \[ a + 5d = 2a \] Let me write that down: \[ a + 5d = 2a \] Then, simplifying: \[ 5d = 2a - a \] \[ 5d = a \] ...middle part omitted... Therefore, the greatest number is 220. ... Further 30 lines omitted... Thus, the greatest number is 220. So I think that's the answer.
RESPONSE gpt-oss-120b
We need to solve: Six terms in arithmetic sequence, with max = 2 * min. Sum = 990. Find max. Let sequence: a, a+d, a+2d, a+3d, a+4d, a+5d, where a is first term (least? Actually could be smallest or largest? It says "greatest number ... is double the least number". In arithmetic sequence, the terms are increasing if d>0. So smallest is a, largest is a+5d. Then a+5d = 2a (since greatest = double least). So a+5d = 2a => 5d = a => a = 5d. So first term a =5d. Then terms are: 5d, 6d, 7d, 8d, 9d, 10d. Indeed smallest 5d, largest 10d = double. Good. Sum = (5d+6d+7d+8d+9d+10d) = (5+6+7+8+9+10)d = (45) d? Let's compute: 5+6=11, +7=18, +8=26, +9=35, +10=45. Yes sum =45 d? Given total sum =990 => 45 d =990 => d=990/45=22? 45*22 = 990 indeed. So d=22. Then greatest number = 10d = 220. Check: smallest =5d=110, largest=220, sum=990. Answer: 220. But ensure integer conditions. Yes. Thus answer: 220. Now produce final answer.
DeepSeek-R1-0528 generates on
average 3,104 reasoning tokens while
gpt-oss-120b generates only 268
for this prompt. We can observe a number of curious
optimizations in the CoT of
gpt-oss-120b:
- It uses extremely abbreviated language, avoiding any unnecessary words.
- Formatting in the CoT is notably reduced, compared to the output: No markdown sequences, very limited use of math formatting.
- Much fewer iterations are used to check the results once they are found.
Logic puzzles
For brevity, only examples of
gpt-oss-120b traces are shown
here.
Original Monty Hall Problem
RESPONSE gpt-oss-120b
We need to answer the classic Monty Hall problem. The answer: you should always swap, because it gives 2/3 chance of winning the car. Provide explanation.
Inverted Monty Hall Problem
RESPONSE gpt-oss-120b
We need to answer: "You're on a game show... three doors: 1 donkey, 2 cars. You pick one. Host opens one of the others revealing a luxury car. Then you can keep or swap. What should you do to win a car?" This is a variation of Monty Hall but with two cars and one donkey. We need to compute probabilities.
Initially, you pick a door randomly. Probability you initially picked donkey = 1/3, car = 2/3. There are two cars and one donkey.
... middle part omitted ...
Thus answer: Keep initial (do not swap). Provide explanation.
Make answer concise.
A very curious finding is that the model is able to distinguish between logic problems where the solution is known from the training data, e.g., the Monty Hall problem, and modified problems that require additional reasoning, such as the inverted Monty Hall problem. It will only initiate a long CoT for the unknown problem.
Model evolution
While we have only looked at recent model variants above, it is also of interest to look at the historic evolution between different reasoning model variants.
The figures below show how the relative completion tokens changed across the different problem domains for iterations of models within the labs.
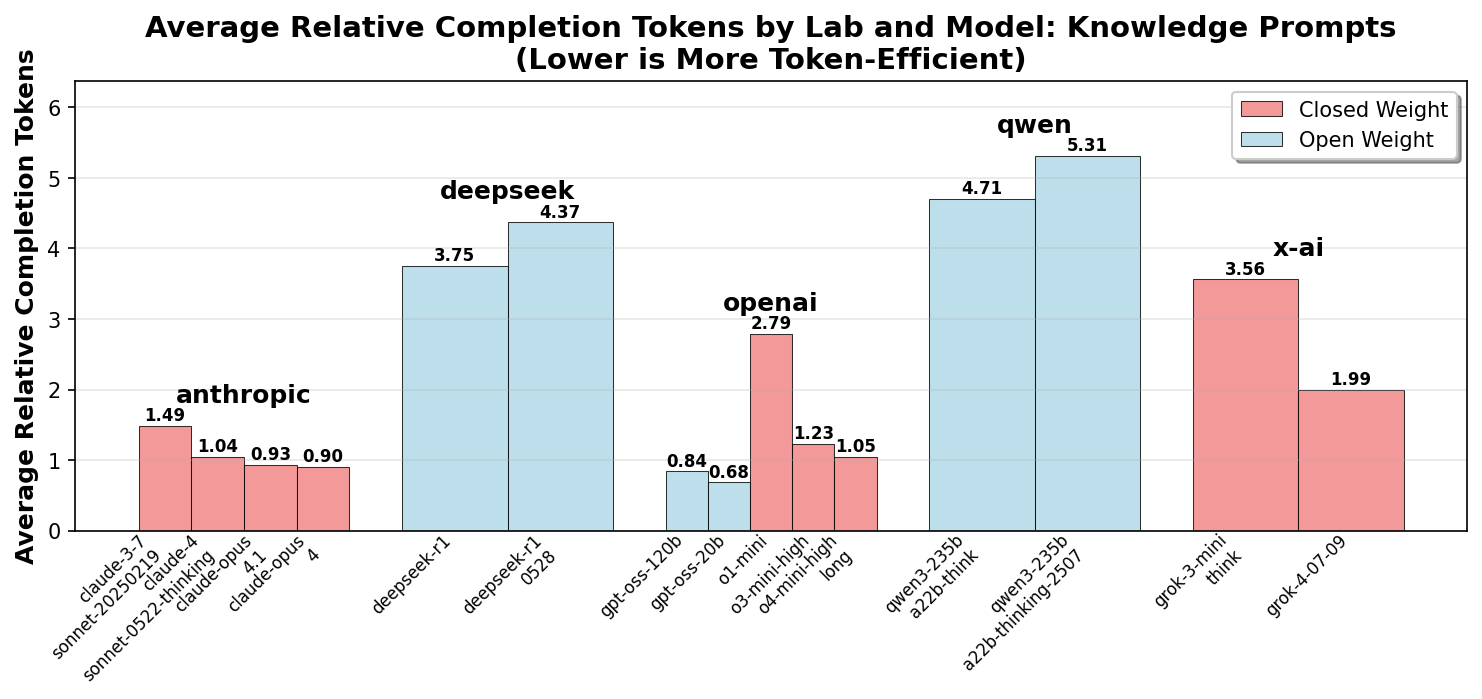
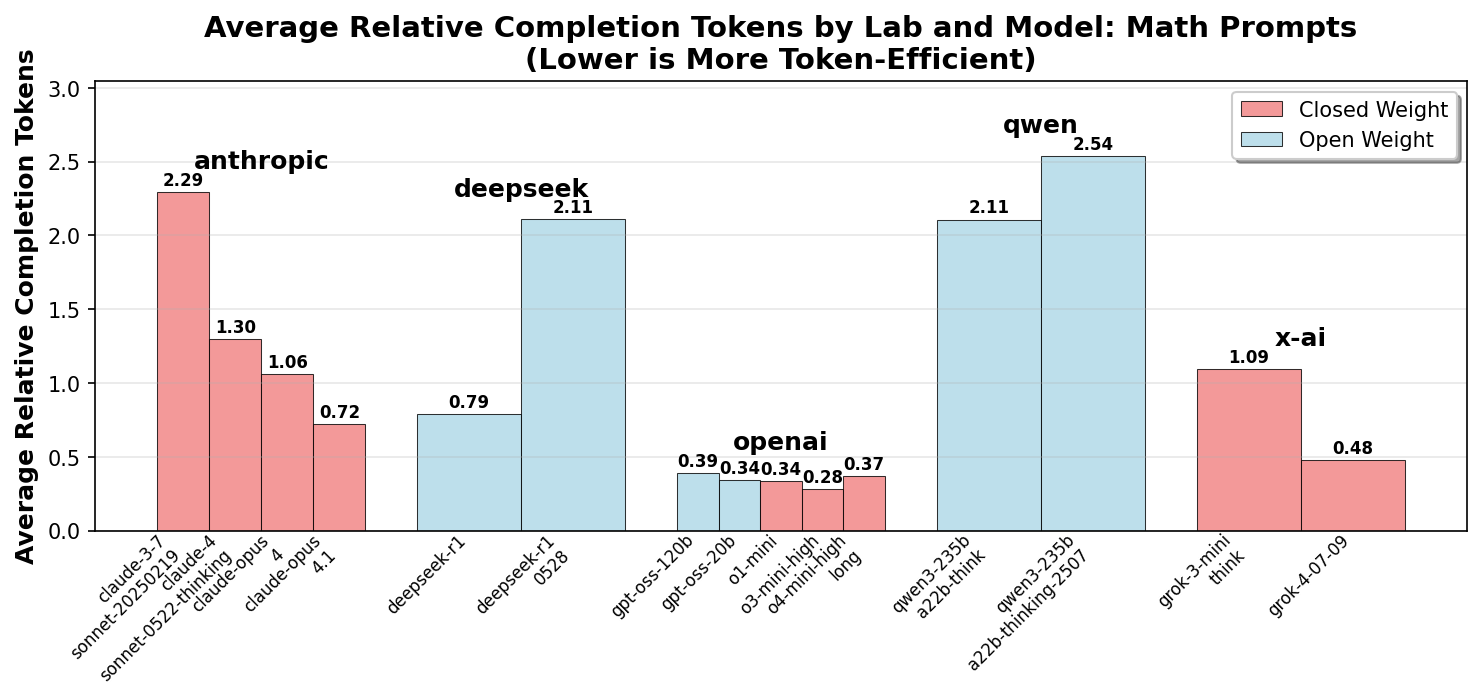
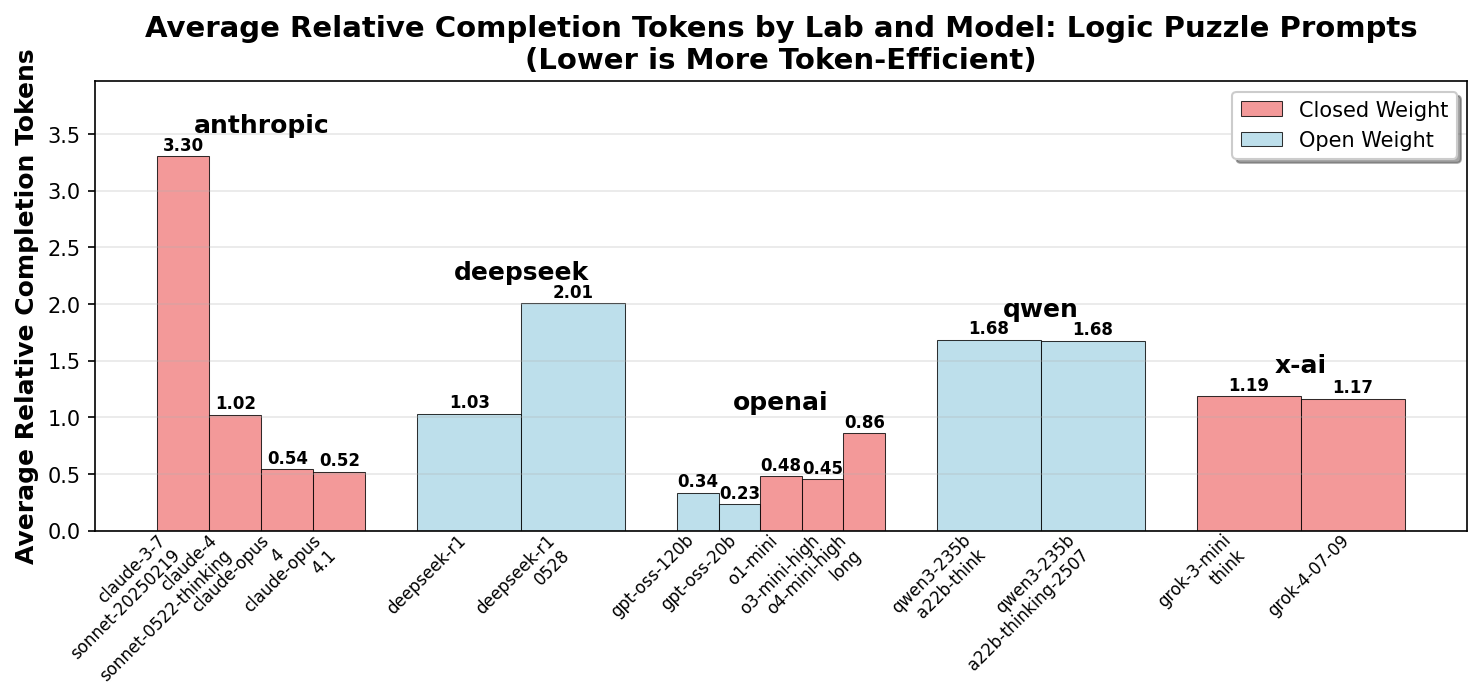
We can observe four key trends:
- Closed weight models have been iteratively optimized to use fewer tokens to reduce inference cost.
- The open weight models (DeepSeek and Qwen) have increased their token usage for newer versions, possibly reflecting a priority toward better reasoning performance.
-
OpenAI models stand out for extreme token efficiency in
math problems, even beginning with o1. It appears that
X-AI is taking a similar approach with
grok-4, with significant improvements compared togrok-3-mini. -
The recently released
gpt-oss-120bandgpt-oss-20bseem to inherit the CoT density optimization from the o-mini models.
Summary
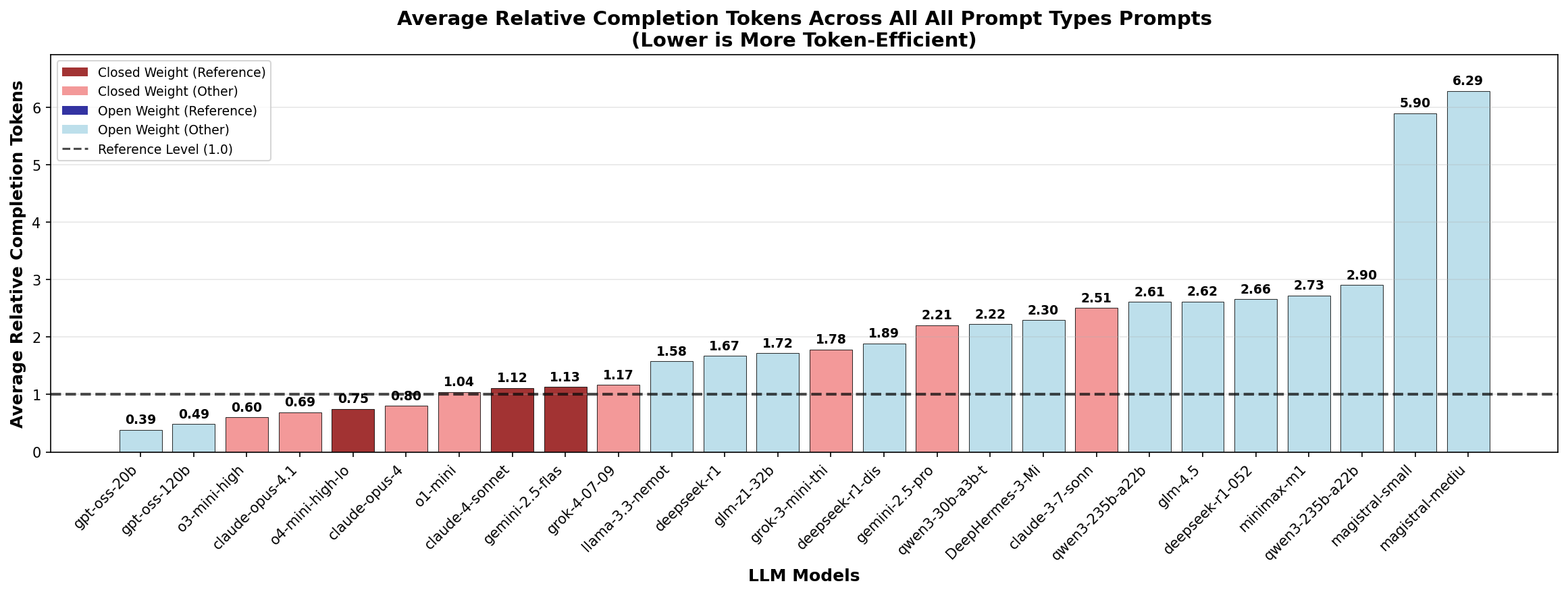
We find that open-weight models use consistently more tokens than closed-weight models for equivalent tasks. However, the efficiency gap depends on the workload and is most pronounced for superfluous reasoning in knowledge questions. On average, 3x more tokens are required for knowledge prompts. The gap reduces to less than 2x for math problems and logic puzzles.
Furthermore, many closed weight models allow steering of the reasoning effort, which provides an effective way to reduce token usage for simple tasks.
llama-3.3-nemotron-super-49b-v1
stands out as the most token efficient open weight model
across all domains prior to the release of the
gpt-oss models, while the
Magistral models represent an unusual outlier toward the
high end.
The recent release of
gpt-oss-120b and
gpt-oss-20b as open weight and
state-of-the-art token efficient reasoning models with
freely accessible CoT could serve as a
reference for further optimization of other models.
We note the continued trend of closed weight reasoning models to improve token efficiency also in non-benchmark domains and suggest this as an important avenue for future open weight models. A more densified CoT will also allow for more efficient context usage and may counter context degradation during challenging reasoning tasks.
Acknowledgments
Thanks to Teknium and Billy for providing feedback on early drafts of this report and encouragement for its creation. Also thanks to Rishav for preparation of the web version from the draft. Nous Research is acknowledged for providing tokens for this investigation.
Methods
General
All models were accessed through OpenRouter, with the exception of Deephermes, which was accessed via the Nous API, and DeepSeek R1-0528, which was accessed through the DeepSeek API. Generation limits were set to 30,000 tokens with reasoning effort configured to "high" in the OpenRouter API. In cases where models timed out before generating the full 30,000 tokens, queries were restarted and the provider was adjusted as needed to ensure completion when the query did not complete initially. Typical reasons for failure to complete were timeouts.
Statistical analysis was conducted with N=5 samples for each prompt and language model combination.
The gpt-oss-120b and
gpt-oss-20b models were accessed
through the OpenAI API on the day of their first release
using Groq as a provider. There is some uncertainty in the
way the API interprets the reasoning effort settings, which
may lead to deviations in the number of reasoning tokens
generated. We will monitor the situation and update the
report if necessary.
Acquiring response and thinking token data
While many models directly provide reasoning token counts through their API responses, we found these numbers to be unreliable in numerous cases. For instance, Anthropic models would only return the length of the transcribed Chain of Thought rather than the actual CoT lengths, while other models would occasionally report CoT lengths that exceeded the total completion length—a logical impossibility.
To address these inconsistencies, our evaluation scripts implemented consistency checks to assess the validity of returned CoT lengths. When the provided reasoning token counts failed validation, we employed fallback estimation methods using the following formulas:
- When CoT text is not available: CoT tokens = Completion tokens - (Answer length in characters / 3.1)
- When CoT text is available: CoT tokens = Completion tokens × (CoT length in characters / completion length in characters)
Model pricing
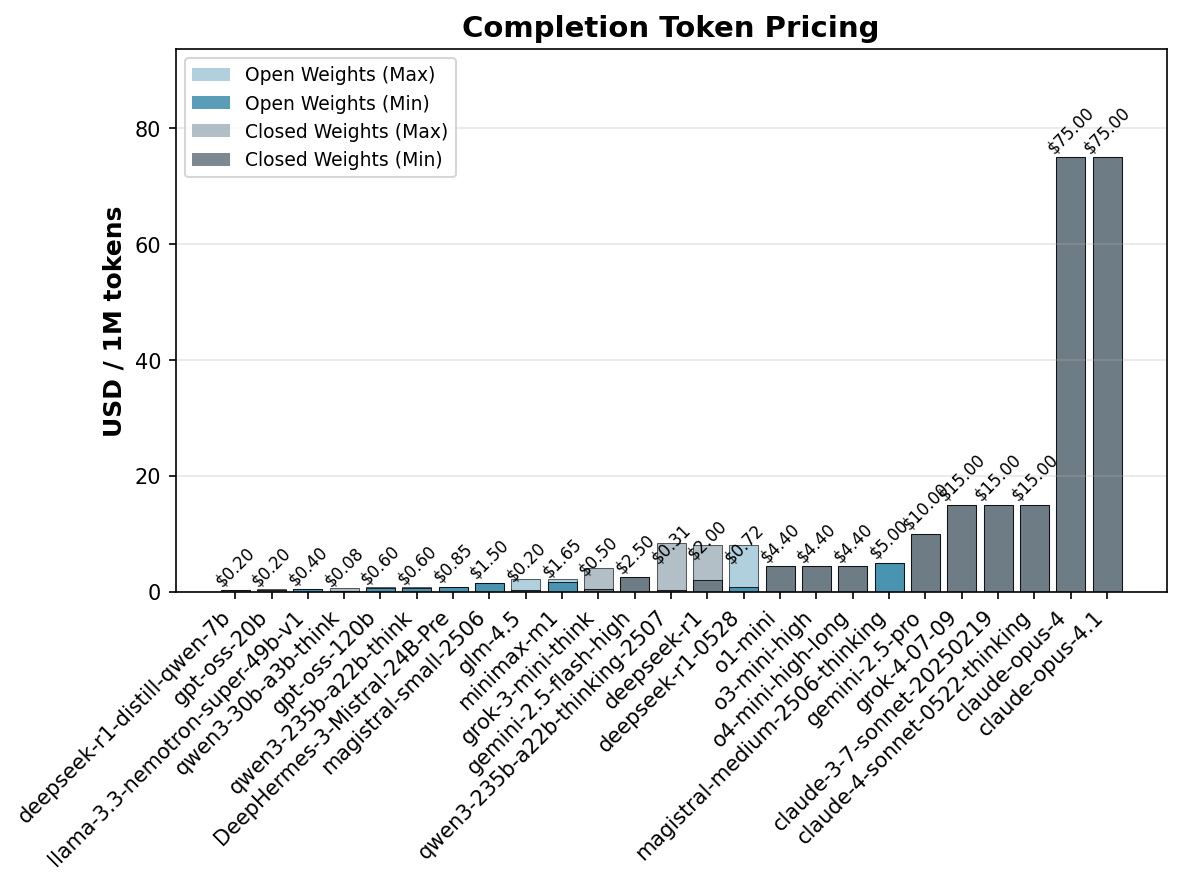
Pricing data for completion tokens (measured in $/1M tokens) was automatically extracted from the OpenRouter API for each model in July 2025, with the exception of Deephermes3. The pricing information captures both minimum and maximum rates available through different providers, as illustrated in Figure A below.

Dataset, harness and evaluation code
All datasets and code can be found in this repository:
(https://github.com/cpldcpu/LRMTokenEconomy/)